Att räkna ut volymen på en cylinder är faktiskt enklare än det kanske låter. Allt du behöver är en enda, kraftfull formel: V = πr²h. Med hjälp av cylinderns radie (r) och dess höjd (h) kan du snabbt ta reda på hur mycket den rymmer. Den här kunskapen är otroligt användbar för att lösa en hel del problem du kan stöta på i vardagen eller på prov.
Hur formeln för en cylinders volym egentligen fungerar
Formeln V = πr²h kan se lite kryptisk ut vid första anblicken, men den bygger på en väldigt logisk princip. Låt oss bryta ner den i två enkla delar.
Först och främst har vi basytan, alltså cylinderns botten, som ju är en cirkel. Arean för just den cirkeln räknar du ut med den välkända formeln πr². Tänk dig att du har räknat ut arean och nu har en helt platt cirkelskiva framför dig.
Nästa steg är att multiplicera den här arean med cylinderns höjd, h. Det är här det blir visuellt. Föreställ dig att du staplar massor av exakt likadana cirkelskivor ovanpå varandra, ända tills stapeln når cylinderns fulla höjd. Volymen är helt enkelt den totala ytan av alla dessa skivor tillsammans. Det är precis därför formeln multiplicerar basytans area (πr²) med höjden (h).
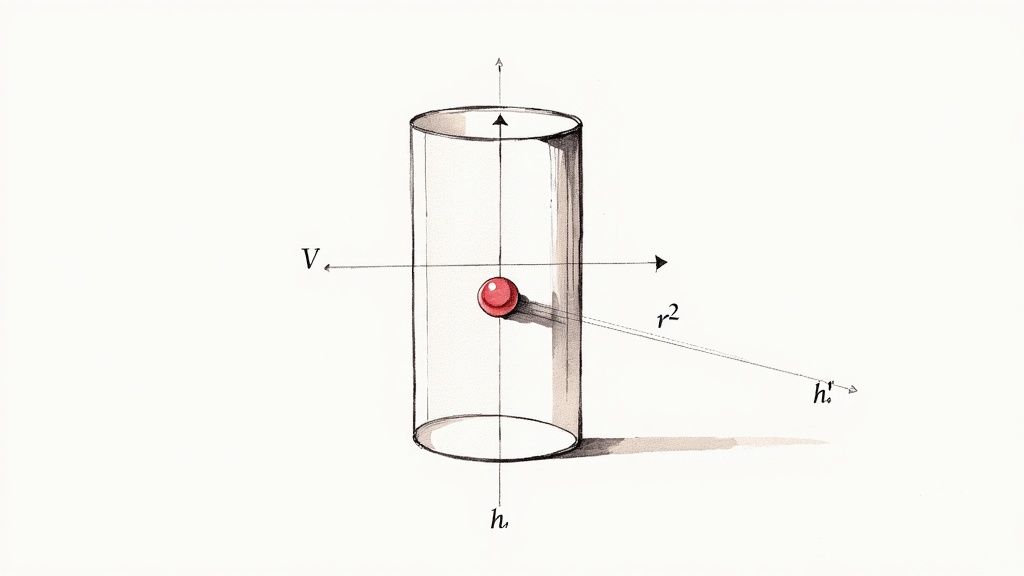
Formelns delar och deras betydelse
För att verkligen kunna använda formeln utan att tveka är det bra att ha stenkoll på vad varje liten del betyder.
Här är en snabb översikt som förklarar varje variabel i formeln V = πr²h och dess specifika roll i uträkningen.
| Variabel | Symbol | Beskrivning | Exempel |
|---|---|---|---|
| Volym | V | Det totala tredimensionella utrymmet inuti cylindern. Svaret anges i kubikenheter (t.ex. cm³). | En vanlig 33 cl läskburk har en volym på ca 330 cm³. |
| Pi | π | En matematisk konstant, ungefär 3,14159. Den beskriver förhållandet mellan en cirkels omkrets och dess diameter. | Används i alla beräkningar som rör cirklar, klot och cylindrar. |
| Radie | r | Avståndet från mitten av cylinderns cirkelformade bas rakt ut till kanten. Radien är alltid hälften av diametern. | Om en burk är 6 cm tvärs över (diameter), är radien 3 cm. |
| Höjd | h | Det vinkelräta avståndet mellan de två cirkelformade basytorna (botten och toppen). | En standardläskburk är ungefär 11,5 cm hög. |
Den här tabellen är ett bra fuskblad att ha till hands när du börjar öva. Snart kommer du kunna delarna utantill.
En grundpelare i svensk matematik
Att kunna räkna ut en cylinders volym är mer än bara en teoretisk övning – det är en grundläggande färdighet i den svenska skolan. Enligt statistik från nationella proven 2023 kunde faktiskt runt 95% av alla niondeklassare hantera den här typen av beräkningar. Lärare använder ofta vardagliga föremål, som just läskburkar eller konservburkar, för att göra matematiken mer konkret och lättare att förstå.
Tänk på det så här: Basytan är grunden, och höjden är hur många lager av den grunden du har. Multiplicera dem, och du får hela byggnadens volym.
Det är ofta viktigare att förstå varför formeln ser ut som den gör än att bara memorera den rakt av. När du sedan ställs inför lite klurigare problem, kanske med enheter som behöver omvandlas eller bråktal inblandade, kommer den här djupare förståelsen hjälpa dig att anpassa din lösningsmetod. Känner du dig lite ringrostig på just bråk kan du fräscha upp minnet med vår guide om att räkna med bråktal.
Praktiska räkneexempel från start till svar
Nu har vi koll på formeln V = πr²h, men teori är en sak och praktik en annan. För att verkligen få grepp om hur man räknar ut en cylinders volym finns det inget som slår att gå igenom ett par konkreta exempel, steg för steg.
Vi börjar med grunderna och bygger sedan på med lite klurigare varianter som du lätt kan stöta på i verkligheten eller på ett prov.
Att jobba igenom några scenarier gör det mycket enklare att se hur man plockar ut rätt information, sätter in den i formeln och hanterar vanliga fallgropar som till exempel enhetsomvandlingar.
Exempel 1: En grundläggande uträkning
Föreställ dig en helt vanlig konservburk. Låt oss säga att den har en radie (r) på 4 cm och en höjd (h) på 10 cm. Nu ska vi beräkna dess volym.
Vi börjar med att ställa upp formeln:
- V = πr²h
Sedan byter vi ut bokstäverna mot siffrorna vi har:
- V = π × (4 cm)² × 10 cm
Nu är det dags att räkna. Kom ihåg räkneordningen – potensen (upphöjt till 2) kommer först.
- V = π × 16 cm² × 10 cm
- V = 160π cm³
För att få ett mer greppbart svar kan vi byta ut π mot dess närmevärde (≈ 3,14159):
- V ≈ 160 × 3,14159 ≈ 502,65 cm³
Så, konservburkens volym är alltså ungefär 502,7 kubikcentimeter om vi avrundar till en decimal.
Exempel 2: När du får diametern istället
Det här är ett klassiskt knep, inte minst på Högskoleprovet. Du får veta att en cylindrisk vattentunna har en diameter på 60 cm och en höjd på 100 cm. Märk väl: du fick diametern, inte radien.
Det absolut första och viktigaste du måste göra är att räkna ut radien.
Tips: Radien är alltid hälften av diametern. Ett av de vanligaste felen är att man av misstag stoppar in hela diametern i formeln, vilket leder till ett helt felaktigt svar.
Så, vi beräknar radien:
- Radie (r) = Diameter / 2 = 60 cm / 2 = 30 cm
Nu kan vi använda formeln precis som i förra exemplet:
- V = πr²h
- V = π × (30 cm)² × 100 cm
- V = π × 900 cm² × 100 cm
- V = 90 000π cm³
Och för att få ett exaktare värde multiplicerar vi med pi:
- V ≈ 90 000 × 3,14159 ≈ 282 743 cm³
Vattentunnans volym är alltså nästan 283 000 kubikcentimeter. Ganska stort, eller hur?
Exempel 3: Från kubikcentimeter till liter
Okej, låt oss ta resultatet från vattentunnan och göra det lite mer användbart. Att säga "282 743 kubikcentimeter" är visserligen korrekt, men det säger oss inte så mycket i praktiken. När vi pratar om vätska är liter en mycket vanligare enhet. Så, hur gör vi omvandlingen?
Nyckeln ligger i att kunna sambandet mellan kubikcentimeter (cm³) och liter (L).
- 1000 cm³ = 1 liter
För att omvandla vår volym till liter behöver vi bara dela med 1000:
- Volym i liter = 282 743 cm³ / 1000 = 282,743 L
Vattentunnan rymmer alltså ungefär 283 liter. Den här sortens enhetsomvandlingar dyker upp hela tiden i uppgifter som rör volym, och är en kritisk färdighet för den kvantitativa delen av Högskoleprovet. För att slipa på dina kunskaper kan du spana in fler lösningsguider för den kvantitativa delen som tar upp fler geometriska problem. Att ha stenkoll på enheterna från början till slut är A och O för att landa på rätt svar.
Vanliga misstag som är lätta att göra (och hur du undviker dem)
Att räkna ut volymen på en cylinder känns oftast ganska rakt på, men det finns några klassiska fällor som är förvånansvärt lätta att falla i. Särskilt när klockan tickar under ett prov som Högskoleprovet.
Men om du känner till de här fallgroparna i förväg är du redan halvvägs till att undvika dem. Se det här som en snabb checklista för att säkra dina uträkningar.
Förväxla radie med diameter
Det här är utan tvekan det allra vanligaste misstaget. Formeln V = πr²h bygger på radien (r), men många uppgifter ger dig medvetet diametern (d) istället för att se om du är uppmärksam.
- Typiskt fel: Du ser en diameter på 10 cm och stoppar in siffran 10 direkt i formeln: V = π × 10² × h.
- Korrekt: Du noterar att radien är hälften av diametern, alltså 10 cm / 2 = 5 cm. Rätt uträkning blir då: V = π × 5² × h.
Ett litet misstag, men det fyrdubblar ditt svar (eftersom 10² är 100 medan 5² bara är 25). Det är alltså helt avgörande att du tar en extra sekund och kollar vad du faktiskt har fått.
Minnesregel: Diametern går hela vägen tvärs över cirkeln. Radien sträcker sig bara från mitten och ut. Använd alltid radien.
Glömma "upphöjt till 2"
När du väl har koll på radien är nästa snubbeltråd att glömma den lilla tvåan i formeln. Att man glömmer att kvadrera radien (alltså multiplicera den med sig själv) händer oftare än man tror.
I en stressad situation är det lätt hänt att hjärnan genar och förenklar formeln till V = π × r × h, vilket leder till ett helt felaktigt svar.
- Exempel: Radien är 4 cm och höjden 10 cm.
- Felaktig uträkning: V = π × 4 × 10 = 40π cm³.
- Korrekt uträkning: V = π × 4² × 10 = π × 16 × 10 = 160π cm³.
Som du ser blir skillnaden enorm. Resultatet blir bara en fjärdedel av det korrekta svaret om du missar kvadreringen.
Slarva med enheterna
En annan klassiker som ställer till det är när måtten anges i olika enheter. Om radien är i centimeter och höjden i meter måste du först omvandla dem så att du räknar med samma enhet.
Tänk dig detta scenario: En cylinder har en radie på 50 cm och en höjd på 2 meter.
- Fel: Att direkt räkna V = π × 50² × 2. Här blandas centimeter med meter, och resultatet blir meningslöst.
- Rätt: Bestäm dig för en enhet och håll dig till den. Vi gör om allt till centimeter: höjden 2 meter blir 200 cm. Nu kan du räkna korrekt: V = π × 50² × 200.
Att vara konsekvent med enheterna från start är A och O för att få ett svar som faktiskt stämmer med verkligheten.
Så används cylinderns volym i verkliga livet
"När kommer jag någonsin att behöva det här?" Det är en klassisk fråga från skolbänken. Men när det gäller att beräkna volymen på en cylinder är svaret faktiskt: oftare än du tror. Kunskapen är långt ifrån bara teoretisk matte, utan ett konkret verktyg som används dagligen i massor av svenska branscher. Formeln V = πr²h blir plötsligt väldigt relevant när man ser den i praktiken.
Tänk dig vardagen. En läskburk, en rulle hushållspapper, ett limstift eller till och med en vattentunna i trädgården. För företagen som tillverkar dessa är volymberäkning helt avgörande. Det handlar om att bestämma rätt förpackningsstorlek och materialåtgång, vilket i sin tur styr allt från produktionskostnader till logistik.
Bygg och anläggning
Inom den svenska byggsektorn är den här formeln helt fundamental. Tänk på alla betongpelare som håller upp broar och fastigheter, eller de kilometerlånga rörsystem för vatten och avlopp som grävs ner i marken. För att beställa rätt mängd betong eller veta exakt hur mycket jord som måste schaktas bort krävs precisa volymberäkningar.
En liten felmarginal i kalkylen kan snabbt leda till kostsamt materialsvinn eller, ännu värre, förseningar som stoppar upp hela projektet. Det är ingen överdrift att kalla detta en kritisk kompetens. Uppskattningsvis är cirka 30% av alla betongkonstruktioner i Sverige cylindriska. Det gör att formeln för cylindervolym är central i över 90% av de byggprojekt som involverar just rör eller pelare. Vill du fördjupa dig mer finns det bra resurser om beräkning av cylindervolym och dess roll i industrin.
Livsmedel och förpackningar
Ta en titt i ditt eget köksskåp. Konservburkar, kryddbehållare och dryckesförpackningar är alla perfekta exempel på där formeln för cylindervolym har varit en nyckel i designprocessen. Livsmedelsproducenter måste hela tiden optimera sina förpackningar.
De behöver säkerställa att förpackningen:
- Rymmer en exakt mängd produkt, till exempel 400 gram krossade tomater.
- Använder så lite material som möjligt för att sänka kostnader och minska miljöpåverkan.
- Går att stapla och transportera effektivt på lastpallar.
En minimal justering av en burks radie eller höjd kan, när den multipliceras med miljontals tillverkade enheter, leda till enorma besparingar för ett företag.
Fler branscher där cylindervolymen är avgörande
Det stannar inte vid bygg och mat. Formeln dyker upp överallt där cylindriska former hanteras.
I tabellen nedan ser du några exempel på hur brett den här kunskapen faktiskt används inom svensk industri.
| Exempel på användningsområden för cylindervolym |
| :--- | :--- | :--- |
| Bransch | Tillämpning | Varför det är viktigt |
| Energi | Lagring i cylindriska tankar (olja, gas) | För att övervaka lagernivåer, planera leveranser och följa säkerhetsföreskrifter. |
| Processindustri | Reaktorer och blandningskärl | För att dosera kemikalier korrekt och säkerställa att processerna fungerar som de ska. |
| VVS | Rördragning och beräkning av flöde | För att dimensionera rörsystem så att de klarar av rätt tryck och vattenmängd. |
| Läkemedel | Tillverkning av piller och kapslar | För att garantera exakt dosering av den aktiva substansen i varje enhet. |
Från stora oljecisterner till små medicinkapslar – principen är densamma. Att kunna räkna ut volymen är helt enkelt en förutsättning för att få jobbet gjort på rätt sätt.
Att beräkna volymen på en cylinder handlar inte bara om att få rätt på ett matteprov. I verkligheten kan det vara skillnaden mellan en bro som står stadigt, en fabrik som har tillräckligt med råmaterial eller en förpackning som är både kostnadseffektiv och hållbar.
När man ser dessa praktiska exempel blir det uppenbart att kunskapen är allt annat än teoretisk. Det är en viktig pusselbit som får stora delar av vårt moderna samhälle att fungera.
Dags att öva inför högskoleprovet
Teori i all ära, men det är när man sätter kunskaperna på prov som de verkligen fastnar. Att nöta uppgifter är oslagbart för att bli snabb och säker, särskilt inför ett tidspressat prov som Högskoleprovet. Här kommer några uppgifter som liknar de du kan stöta på.
Vissa är ganska raka på sak, medan andra kräver att du tänker till lite extra – kanske genom att räkna baklänges för att hitta en höjd eller en radie. Se det som ett perfekt genrep.
Uppgift 1: En enkel start
En helt vanlig cylindrisk mugg har en inre radie på 3,5 cm och är 9 cm hög. Hur många kubikcentimeter (cm³) vätska rymmer den? Svara med en decimals noggrannhet.
Uppgift 2: Håll koll på diametern och enheterna
Ett cylindriskt rör har en yttre diameter på 80 mm och en längd på 1,2 meter. Beräkna rörets totala volym i kubikcentimeter (cm³) och avrunda till närmaste heltal. Glöm inte att göra om alla mått till samma enhet först!
Det här är ett klassiskt knep på prov – att blanda enheter och ge dig diametern istället för radien. Om du vill bli van vid den här typen av problem är det guld värt att öva på riktiga prov. Du hittar massor av gamla HP-prov att öva på för att se precis hur vanliga de är.
Uppgift 3: Tänk baklänges
En cylindrisk tank rymmer exakt 785 liter. Radien på tankens botten är 50 cm. Hur hög är tanken, angivet i meter? Du kan använda närmevärdet π ≈ 3,14 för den här uträkningen. (Tips: 1 liter motsvarar 1000 cm³).
Att kunna stuva om i formeln V = πr²h för att lösa ut höjden eller radien är en riktigt värdefull färdighet. Det visar att du förstår principerna på djupet, inte bara hur man stoppar in siffror i en färdig mall.
Facit och lösningar
Här nedanför kan du se hur man löser uppgifterna steg för steg. Jämför med dina egna uträkningar och se var du landade.
Lösning 1:
- Vi använder formeln: V = πr²h
- Sätt in värdena: V = π × (3,5)² × 9
- Beräkna: V = π × 12,25 × 9 = 110,25π. Med en miniräknare blir det ungefär 346,4 cm³.
Lösning 2:
- Först, enhetsomvandling: Diametern 80 mm blir 8 cm. Höjden 1,2 m blir 120 cm.
- Sen, från diameter till radie: Radien är hälften av diametern, alltså 8 cm / 2 = 4 cm.
- Sätt in i formeln: V = π × 4² × 120 = π × 16 × 120 = 1920π. Avrundat blir det cirka 6032 cm³.
Lösning 3:
- Gör om volymen: 785 liter är samma sak som 785 × 1000 = 785 000 cm³.
- Möblera om formeln för att lösa ut höjden: h = V / (πr²)
- Stoppa in siffrorna: h = 785 000 / (3,14 × 50²) = 785 000 / (3,14 × 2500).
- Räkna vidare: h = 785 000 / 7850 = 100 cm.
- Omvandla till meter: 100 cm är lika med 1,0 meter.
Vanliga funderingar när du räknar på cylindrar
När man börjar få grepp om formeln för en cylinders volym dyker det ofta upp några kluriga specialfall. Låt oss reda ut de vanligaste frågorna så att du känner dig helt säker.
Spelar det någon roll om cylindern ligger ner?
Kort sagt: nej, det gör det inte. Formeln V = πr²h är precis lika giltig oavsett hur cylindern är orienterad.
Det viktiga är att hålla isär begreppen:
- Höjden (h) är alltid det vinkelräta avståndet mellan de två cirkulära basytorna.
- Radien (r) är avståndet från mittpunkten ut till kanten på en av dessa cirklar.
Tänk dig en liggande vattentank. Det vi i dagligt tal skulle kalla för tankens "längd" är i själva verket "höjden" i formeln. Så länge du korrekt identifierar radien och avståndet mellan de två ändarna kommer du att få fram rätt volym.
Hur räknar man ut volymen på en halv cylinder?
Det här är en klassisk uppgift som ofta dyker upp på prov. Om du till exempel ska räkna ut volymen på ett vattentråg eller ett växthus som är format som en liggande cylinder som kluvits på längden, är metoden enkel.
Du börjar med att räkna ut volymen för hela cylindern med den vanliga formeln, V = πr²h. Därefter delar du helt enkelt svaret med två.
Formeln blir alltså V = (πr²h) / 2. Lätt att räkna ut, men också lätt att glömma det där sista steget i stridens hetta.
Vilket värde ska jag egentligen använda för pi?
En ständig fråga! Svaret beror helt på sammanhanget och vilka hjälpmedel du får använda.
- På Högskoleprovet: I uppgiftsbeskrivningen står det ofta att du ska använda närmevärdet 3,14. Läs noga!
- Med miniräknare: Använd alltid miniräknarens inbyggda pi-knapp (π). Då får du maximal precision i din uträkning.
- För snabb överslagsräkning: Ibland kan det räcka att avrunda pi till 3 för att få en snabb uppskattning. Var bara medveten om att detta ger ett ganska grovt svar.
Mitt bästa tips är att alltid läsa instruktionerna noga. Om inget specifikt värde anges är det bäst att använda ett så exakt pi som möjligt och sedan avrunda ditt slutsvar enligt de regler som gäller för uppgiften.
